ローンを使う投資はどれくらい危ないのか？モンテカルロ・シミュレーションで見るリスクとリターン

Dec 5, 2025

不動産投資では、ローンを組むことが半ば当たり前になっています。一方で、株や投資信託については「借金して投資するな」というのが一般的なアドバイスですし、私もその考えに賛成です。借入は危険だからということもありますが、それよりも、借り入れるコストに対して期待できるリターンが見合わないからです。

とはいえ、インフレにおいては借り入れた分を返す時にはお金の価値が下がっている、ということもあり、「もし借金して投資したら、実際どうなるのだろう？」というほんの少し思いました。

感覚的にも実際問題としても「株や投資信託は無借金に限る」とわかっていても、**具体的にどれくらい割に合わないのか（もしくは常識に反して思ったよりいいのか）**を数字で見てみたい。そこで、シミュレーションで検証してみることにしました。

この記事では、モンテカルロ・シミュレーションを使って、「借入あり」と「借入なし」の投資を比較します。単一のシナリオではなく、あり得る未来のバリエーションをたくさん生成し、リターンの分布（特にワーストシナリオ）を見ることで、レバレッジ投資のリスクを定量的に考えます。

注意：この記事では「借金はやめとけ」というようなことを掘り下げる手段としてシミュレーションをするということを取り上げるだけであって、レバレッジ投資を勧めるものではありません。

そもそもなぜシミュレーションをしようと思ったのか？

よく「借金して投資はするな」と言われています。借金すると精神的な余裕がなくなるから、というのはよく聞く話ですし、実際その通りだと思います。また、個人が借入する場合、金利が高くなる傾向があります（フリーローンの金利相場は年3〜15%程度）。借入コストが期待リターンを上回りやすいという点も理解できます。

ただ、ある知人が「ローンを組んで投資した。借入額は自分の金融資産の一部を売れば返せる程度だし、インフレ下では借りる方が得」と言っていました。「普通に」考えればそんなはずはない……と思いつつも、シミュレーションしてみたら意外と「なくはない？」という結果になるかもしれない、と少し気になりました。

そこで、感覚や一般論ではなく、数字で確かめてみようと思い立ったのがこの記事のきっかけです。

シミュレーションの設定

まず、比較のための前提条件を整理します。

共通の前提

項目	値
元本（借入額 / 投資対象の初期価格）	200万円
ローン金利（年率）	8%
ローン期間	288ヶ月（24年）
キャピタルゲイン税率	20.315%

2つのシナリオ

シナリオA：借入あり（レバレッジ投資）

200万円を借り入れ、初月に一括で資産を購入
毎月、元利均等返済でローンを返済
任意の時点で売却した場合、売却額からローン残高と税金を差し引いた額が手元に残る

シナリオB：借入なし（積立投資）

借入はしない
シナリオAと同じ「毎月の支払い額」を、毎月の積立投資に充てる
同じ資産を、毎月の価格で購入していく（ドルコスト平均法）

この設定により、毎月のキャッシュアウトは両シナリオで同じになります。つまり、「同じ負担で、どちらの方法が有利か？」を比較できます。

元利均等返済の数学

シナリオAの毎月返済額は、元利均等返済の公式で計算します。

元本を $P$ 、月利を $r$ 、返済回数を $n$ とすると、毎月の返済額 $M$ は：

M = P \cdot \frac{r(1+r)^n}{(1+r)^n - 1}

例えば、 $P = 2,000,000$ 円、年利 8%（月利 $r = 0.08/12 \approx 0.00667$ ）、 $n = 288$ ヶ月の場合：

M \approx 15,641 \text{ 円}

この約15,641円が、シナリオAでは毎月のローン返済額、シナリオBでは毎月の積立投資額になります。

返済の内訳

毎月の返済額 $M$ は、利息部分と元本返済部分に分かれます。

$t$ ヶ月目の返済において：

利息: $I_t = B_{t-1} \cdot r$ （前月末のローン残高 $B_{t-1}$ に月利をかける）
元本返済: $P_t = M - I_t$
新しいローン残高: $B_t = B_{t-1} - P_t$

返済初期は利息の割合が大きく、後半になるほど元本返済の割合が増えていきます。

価格変動のモデル化

資産価格がどう動くかをモデル化する必要があります。ここでは、月次リターンが**独立同分布（i.i.d.）**に従うと仮定します。

正規分布モデル

最もシンプルなモデルは、月次リターン $r_t$ が正規分布に従うというものです：

r_t \sim \mathcal{N}(\mu, \sigma^2)

ここで $\mu$ は月次の期待リターン、 $\sigma$ は月次のボラティリティです。

年率リターン 8%、年率ボラティリティ 15% を想定する場合：

\mu = (1 + 0.08)^{1/12} - 1 \approx 0.0064

\sigma = 0.15 / \sqrt{12} \approx 0.0433

価格指数 $S_t$ は：

S_t = S_{t-1} \cdot (1 + r_t)

ファットテイル：t分布とレヴィ安定分布

現実の金融市場では、正規分布が予測するよりも極端な値動きが頻繁に起こります。これを「ファットテイル」と呼びます。

これを表現するため、以下の分布も試します：

t分布

自由度 $\nu$ のt分布は、正規分布より裾が厚くなります。自由度が小さいほど極端な値が出やすくなります。

r_t \sim t_\nu(\mu, \sigma)

レヴィ安定分布

さらに極端なファットテイルを表現できる分布です。安定性指数 $\alpha$ （ $0 < \alpha \leq 2$ ）が小さいほど裾が厚くなります。 $\alpha = 2$ のとき正規分布と一致します。

r_t \sim \text{Stable}(\alpha, \beta, \mu, \sigma)

モンテカルロ・シミュレーションとは

モンテカルロ・シミュレーションは、確率的なシナリオを大量に生成し、結果の分布を調べる手法です。

価格パスをランダムに1本生成する
そのパスに対して、シナリオA（借入あり）とシナリオB（借入なし）の結果を計算する
1〜2を何百回、何千回と繰り返す
最終的な資産額や利益の分布を分析する

これにより、「平均的にはどうなるか」だけでなく、「最悪の場合どうなるか」「どのくらいの確率で損失が出るか」といったリスクの全体像が見えてきます。

シミュレーションの実装

ここでは、シミュレーションの核となる部分を抜粋して説明します。完全なコードは Gist で公開予定です。

借入ありシナリオの計算

def simulate_investment_with_loan(
    principal: float,
    annual_rate: float,
    loan_months: int,
    price_index: np.ndarray,
    tax_rate: float = 0.20
) -> pd.DataFrame:
    # 価格指数を初期値で正規化
    price_index_adjusted = price_index / price_index[0]
    n_months = len(price_index_adjusted) - 1
    r_m = annual_rate / 12.0

    # 毎月返済額（元利均等）
    if r_m > 0:
        pay = principal * (r_m * (1 + r_m)**loan_months) / ((1 + r_m)**loan_months - 1)
    else:
        pay = principal / loan_months

    # 資産の時価
    property_value = principal * price_index_adjusted

    # 各月のローン残高、利息、元本返済、キャッシュフローを計算
    # ... (詳細は Gist 参照)

    # 売却後税引きリターン = 累積キャッシュフロー + (売却額 - ローン残高 - 税金)
    return df

ポイントは、売却後税引きリターンの計算です：

\text{売却後リターン} = \sum_{t=1}^{T} \text{CF}_t + \left( S_T - B_T - \max(S_T - P, 0) \cdot \tau \right)

ここで $\text{CF}_t$ は $t$ 月のキャッシュフロー（返済額のマイナス）、 $S_T$ は売却時の資産価値、 $B_T$ はローン残高、 $P$ は元本、 $\tau$ は税率です。

借入なしシナリオの計算

def simulate_investment_noloan_with_savings(
    principal: float,
    annual_rate: float,
    loan_months: int,
    price_index: np.ndarray,
    tax_rate: float = 0.20
) -> pd.DataFrame:
    # 借入ありと同じ毎月投資額を計算
    # 毎月、その時点の価格で口数を購入
    # 累積口数 × 現在価格 = 資産価値
    # ... (詳細は Gist 参照)
    return df

モンテカルロの実行

def monte_carlo_comparison(
    principal=2_000_000,
    annual_rate=0.08,
    loan_months=288,
    n_scenarios=500,
    n_months=288,
    mu=0.002,
    sigma=0.01,
    tax_rate=0.20,
    dist_type="normal",  # "normal", "t", "levy"
    t_df=3,
    levy_alpha=1.7,
    levy_beta=0
):
    results_loan = []
    results_noloan = []

    for s in range(n_scenarios):
        # 分布に応じて月次リターンを生成
        if dist_type == "normal":
            shocks = np.random.normal(mu, sigma, n_months)
        elif dist_type == "t":
            shocks = t.rvs(df=t_df, loc=mu, scale=sigma, size=n_months)
        elif dist_type == "levy":
            shocks = levy_stable.rvs(levy_alpha, levy_beta, loc=mu, scale=sigma, size=n_months)

        # 価格パスを生成
        price_index = np.concatenate([[1.0], np.cumprod(1 + shocks)])

        # 両シナリオを計算
        df_loan = simulate_investment_with_loan(...)
        df_noloan = simulate_investment_noloan_with_savings(...)

        results_loan.append(df_loan)
        results_noloan.append(df_noloan)

    return results_loan, results_noloan

シミュレーション結果の読み方

シミュレーション結果は、時系列プロットで可視化します。各月における資産価値や利益の分布を、以下のように表示します：

実線: 平均値
破線: 中央値
帯: 5〜95%区間

帯の幅が広いほど、結果のばらつき（リスク）が大きいことを意味します。

結果から見えること

正規分布の場合

年率リターン 8%、ボラティリティ 15% の正規分布で 500 シナリオを生成した結果：

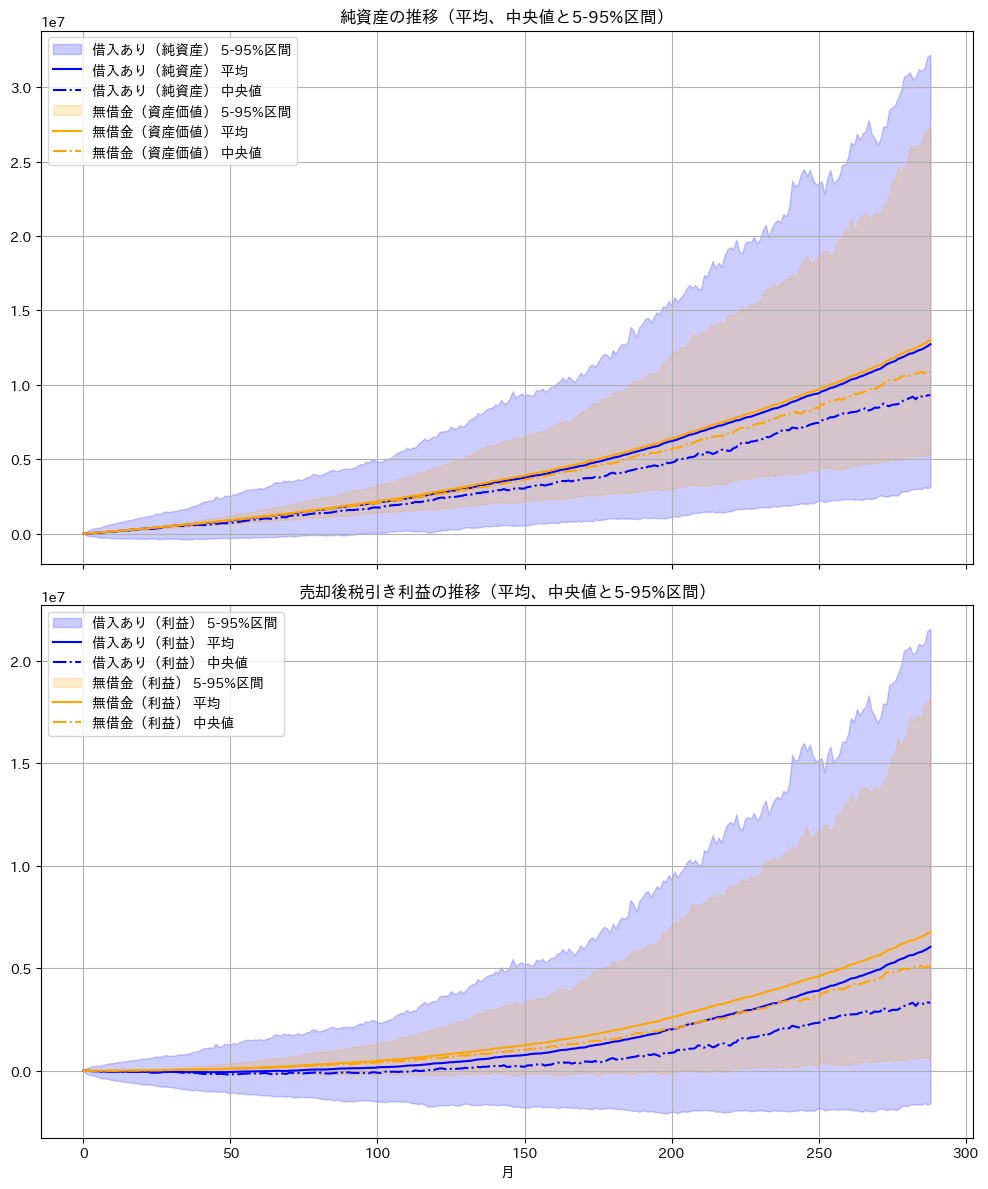
t分布の場合

年率リターン 8%、ボラティリティ 15% のt分布で 500 シナリオを生成した結果：

借入ありのワーストシナリオがさらに悪化する
極端な下落が起きたとき、ローン残高は減らないのに資産価値だけが急落するため、純資産が大きくマイナスになり得る

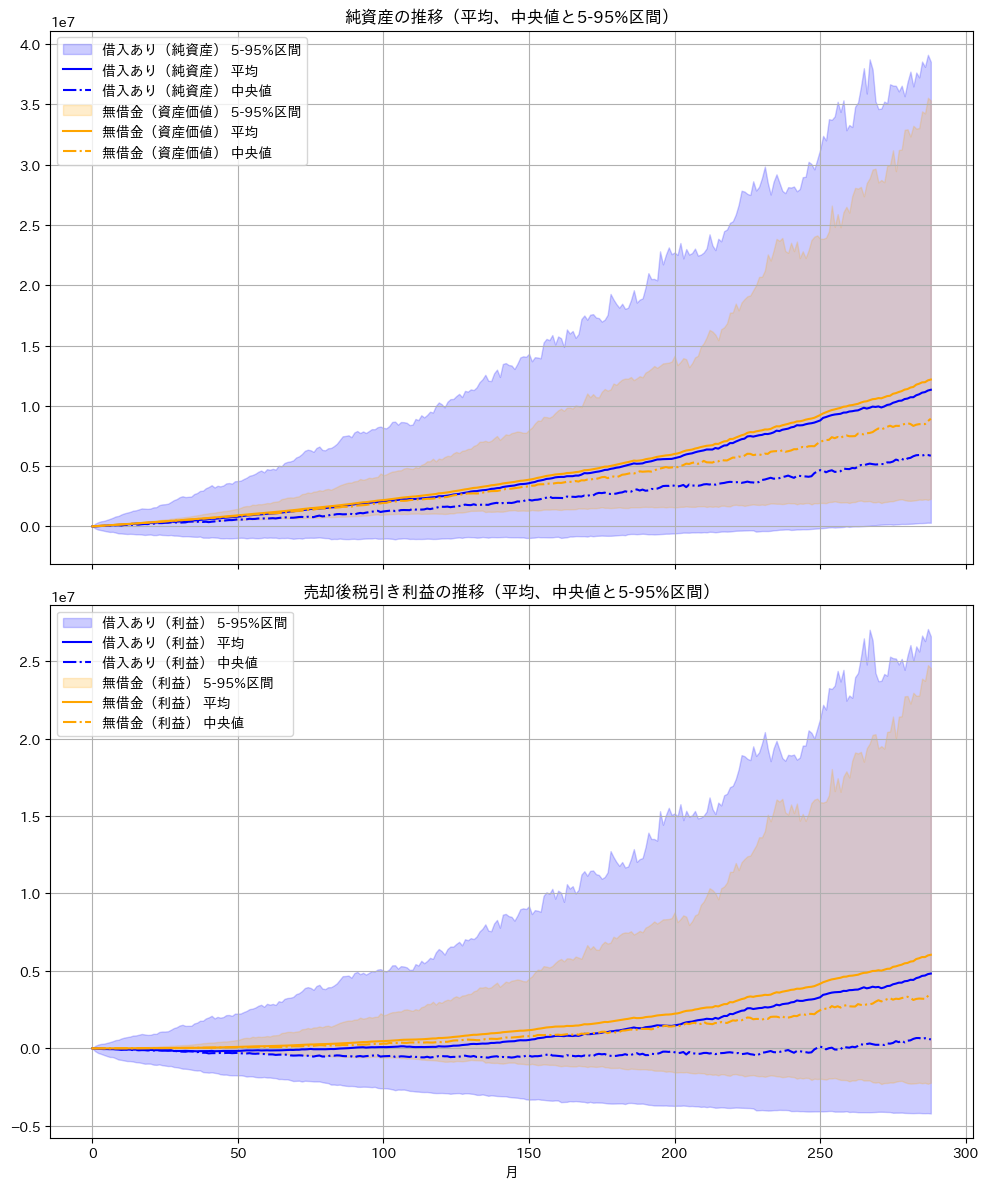
レヴィ分布の場合

年率リターン 8%、ボラティリティ 15% のレヴィ分布で 500 シナリオを生成した結果：

レヴィ分布は極端な価格変動をより頻繁に引き起こすため、借入によるリスクがさらに大きくなります。（リスクが大きいということは、「当たれば」大きく利益が出るということでもありますが、、）

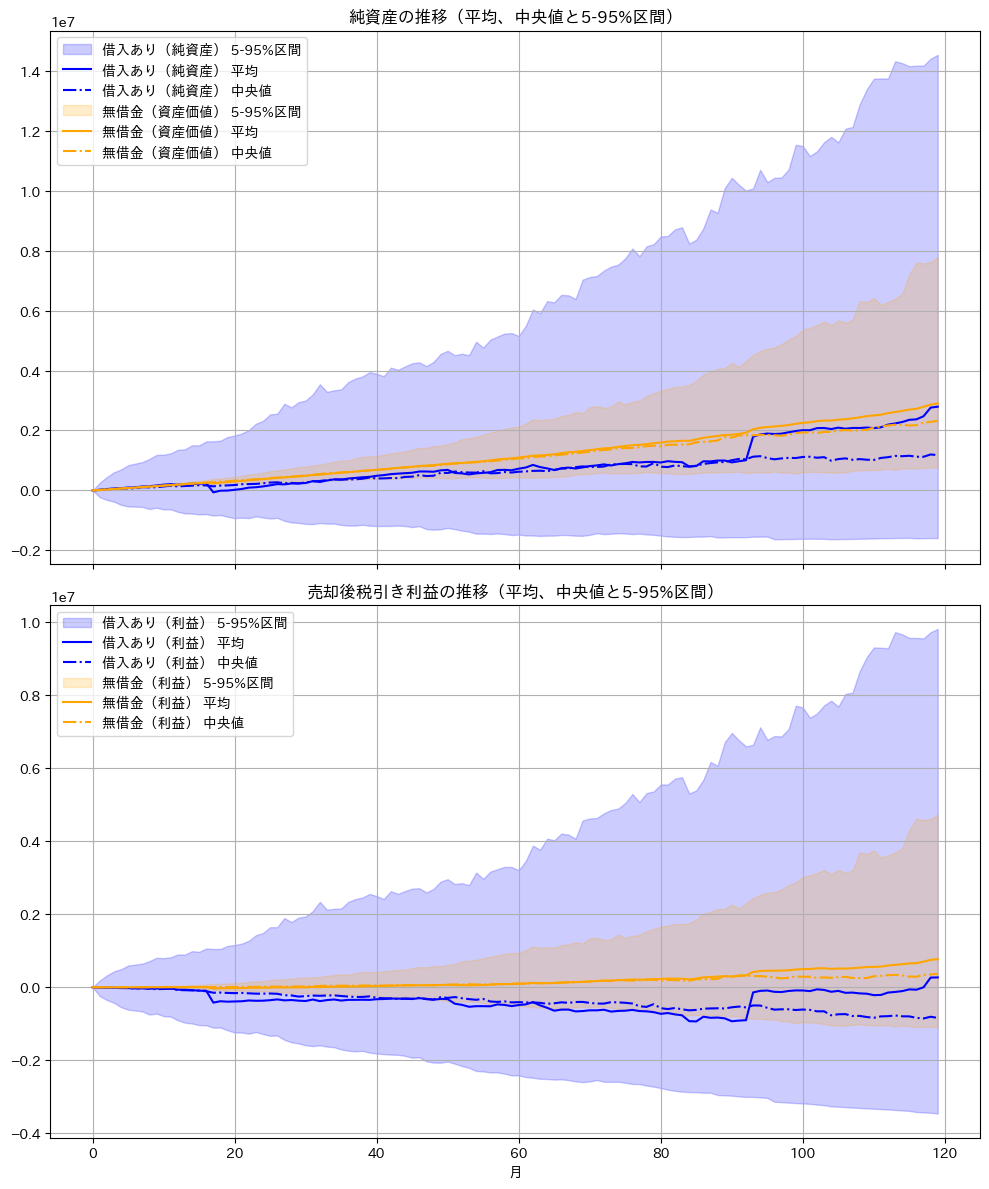
その他のシミュレーション結果について

その他のシミュレーション結果は Gist の方をご覧ください。金利を変えてシミュレーションした結果や、モンテカルロではありませんが実際のデータを使った検証も掲載しています。

まとめ

この記事では、ローンを使った一括投資と、同じ負担での積立投資を、モンテカルロ・シミュレーションで比較しました。よく「投資は借金してはいけない」と言いますし、一方で「借入はレバレッジで、うまく使えば短期間で大きく稼げる」などという場合もありますが、実際にシミュレーションしてみることで、借入によるリスクとリターンのバランスを客観的に把握できます。

で、実際シミュレーションしてみて、「意外とあり？」と思ったかというと、やはり借入はしないほうがいいと思いました。その点については改めて別の記事に書こうかと思いました。